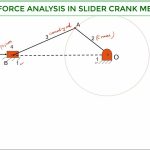
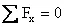From Newton’s First Law, a body is in static equilibrium if the resultant of all the forces (excluding the inertia forces) acting on a rigid body is zero. This condition results in two vector equations:
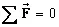
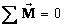
In space, these two vector equations yield six scalar equations:
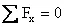 ,
, 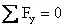 ,
, 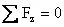
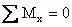 ,
, 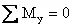 ,
, 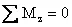
In case of coplanar force systems, there are three scalar equations:
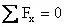 ,
, 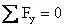 ,
, 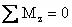
Usually the subscript z in Mz is dropped in coplanar force systems and M implies the moment perpendicular to the plane of the forces.
Static equilibrium equations in space will permit the determination of six unknowns in spatial systems and three unknowns in planar systems.
In coplanar force systems under which the body acted on is in equilibrium, we can have the following force systems:
a) Two-force member: A rigid body acted on by two forces is in static equilibrium only when the two forces are collinear and equal in magnitude but in opposite sense . If the point of application of the two forces are known (points A and B), the direction of these forces will be along the line joining the points of application.
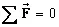
b) Two force and one moment member: A rigid body acted on by two forces and a moment is in static equilibrium only when the two forces form a couple whose moment is equal in magnitude but in opposite sense to the applied moment.
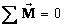
c) Three-force member: A rigid body acted on by three forces is in equilibrium only if the forces are concurrent (intersect at one point). Let the force FA be completely specified. And the line of action of FB and the point of application of FC be known (In plane there are three equilibrium equations and one must have three unknowns to be able to solve the equilibrium equations). When the moment equilibrium equation is written for the sum of moments about the point of intersection of the line of action of FA and FB (point O), since åMO=0, the moment of FC about O must be zero, or the line of action of the force FC must pass through point O. The magnitudes of the forces can then be determined from the force and moment equilibrium equations.