A machine system is considered to be a system of an arbitrary group of bodies (links), which will be considered rigid. We are involved with different types of forces in such systems. Note that when the word “force” is discussed it will refer to a “generalised force” which will also include moments.
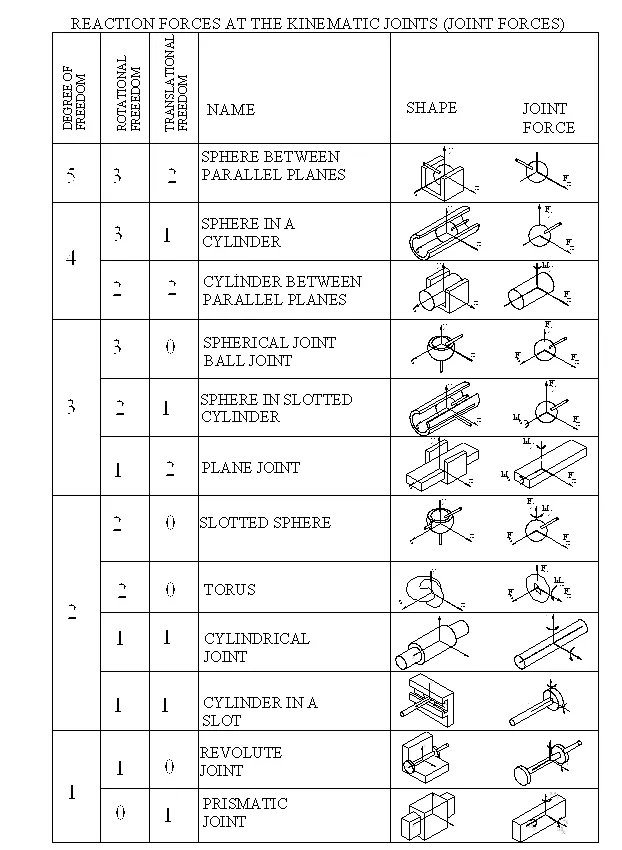
a) Reaction Forces: are commonly called the joint forces in machine systems since the action and reaction between the bodies involved will be through the contacting kinematic elements of the links that form a joint. The joint forces are along the direction for which the degree-of-freedom is restricted. e.g. in constrained motion direction. For example, consider a revolute joint in a planar mechanism. In such a joint there is a rotational freedom and any moment along the axis of the revolute joint will not be transmitted from one link to the other, but there will be a force transmission in any general direction which will be determined by the forces acting on the links. If the revolute joint is in a spatial mechanism, there will be moment reaction components perpendicular to the revolute joint axis and a force reaction in a general direction (e.g. there will be three force components and two moment components). In case of a prismatic joint in a planar mechanism there will be no reaction force component along the axis of the slide but a force perpendicular to the slider axis and a couple along the z-axis will be transmitted between the links joined. In the following table the reaction forces for different joints are shown. If such joints are used in planar mechanisms, the corresponding force and moment components may be considered to be zero (e.g. Fz = 0, Mx = 0 and My =0 in planar mechanisms). (In practice, these reaction components are not necessarily zero and a planar mechanism forms a statically indeterminate system. However, the magnitudes of these force components will be much smaller than the other force components and the error made by neglecting these force components is quite small if the mechanism is designed accordingly). In the joint forces, due to action and reaction, there are two links that are involved. As a convention we denote the joint force Fij (Mij for the couple) as that force acting on link j due to the reaction of link i. hence, from Newton’s third law: Fij = -Fij
b) Physical Forces : As the physical forces acting on a rigid body we shall include external forces applied on the rigid body, the weight of the rigid body, driving force, or forces that are transmitted by bodies that are not rigid such as springs or strings attached to the rigid body. In case of springs, the magnitude and the direction of the force acting will depend on the geometry of the mechanism at the instant considered. In case of a string, when the string is tight, the force will be in the direction of the string and its sense must be such that it keeps the string in tension; otherwise the string force will be zero.

In machine systems, if the force distribution within the rigid body considered is not our concern, the weight of the rigid body can be considered to be equivalent to a force applied at the center of gravity of the rigid body, in the sense and direction of the gravity field.
c) Friction or Resisting Force: In general the resisting forces are those that result due to motion and which resist the motion. Since the rigid body assumption is made, one can neglect the internal friction forces that will exist within the body. In such a case friction forces are at the joints in the direction of the relative motion but in opposite sense or in the members that are specially designed to create the friction force (dampers). Friction forces will be discussed in more detail in coming section .
d) Inertial Forces. Are the forces due to the inertia of the rigid bodies involved. These forces will be discussed in the coming sections.
5.1.4 Free-Body Diagram
In machine systems there are several rigid bodies. A free-body diagram is a sketch of a rigid body or a group of rigid bodies in which all the forces and moments acting on the rigid body are shown. Note that a free-body may involve one link, several parts of a machine or the whole machine. In the free-body diagram both the known forces and the unknown forces are sketched. This diagram need not be in a certain scale, but neatness in such diagrams is essential for a clear understanding. As an example, consider a rigid body, i, as shown. It is connected to other rigid bodies. In the free-body diagram of link i, this body is isolated from other rigid bodies and all the forces (reaction forces, Fki, Fji, Mji ; external forces Fli’, Fli “) are shown. If the magnitude and/or the direction of a force is known, it is indicated.

Please remember that for a solution, a correct free-body diagram is essential. Using this free-body diagram one can easily determine the necessary mathematical approach for the solution. The known values and unknown values in the problem can easily be identified.
In performing the static and dynamic force analysis of machinery, almost always the free-body diagram of each rigid body is drawn and the known forces are identified. One has to solve for the remaining unknown.