The Grashof’s law states that for a four-bar linkage system, the sum of the shortest and longest link of a planar quadrilateral linkage is less than or equal to the sum of the remaining two links, then the shortest link can rotate fully with respect to a neighboring link.
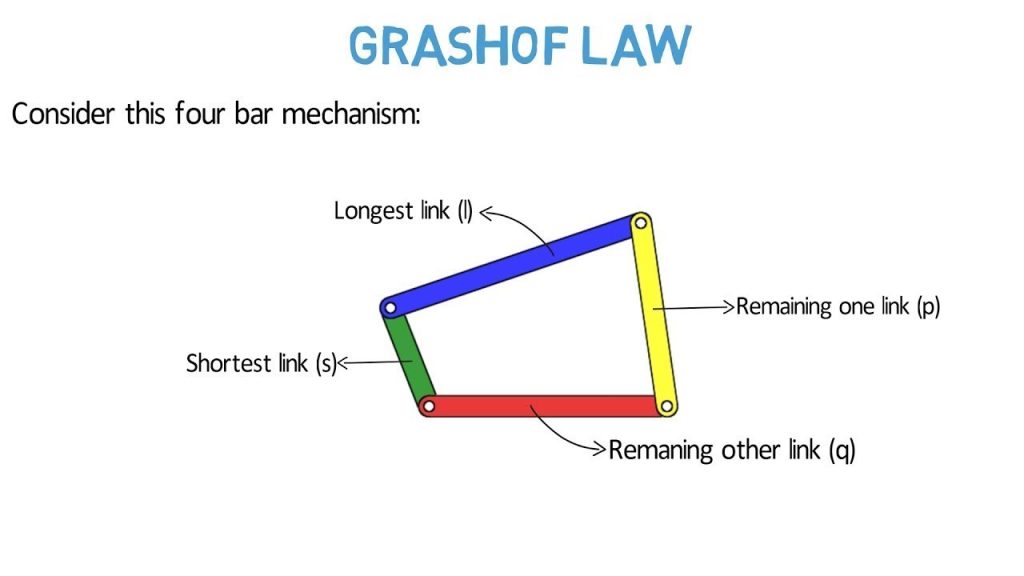
Consider a four-bar-linkage. Denote the smallest link by S, the longest link by L and the & other two links by P and Q.
If the Grashof’s Law condition is satisfied i.e S+L ≤ P+Q,
then depending on whether shortest link ‘S’ is connected to the ground by one end, two ends, or no end there are 3 possible mechanisms. They are:
1. Double crank mechanism
2. Double-rocker mechanism and
3. Crank and Rocker Mechanism
1. Double crank mechanism
In double crank mechanism, the shortest link ‘S’ is a ground link. Both input crank and output crank rotate at 360°.
Grashof’s condition for double crank mechanism: s+l > p+ q
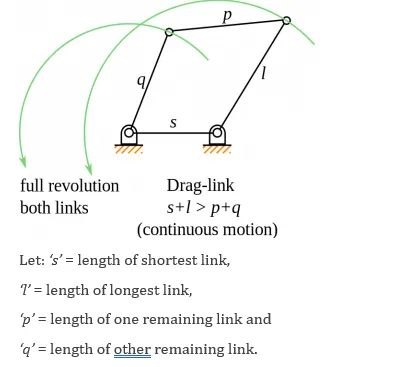
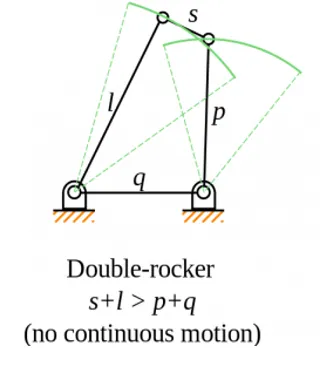
2. Double-rocker mechanism
In double-rocker mechanism, the shortest link ‘S’ is coupler link. The coupler link can rotate 360°.
Grashof’s condition for double crank mechanism: s+l > p+ q
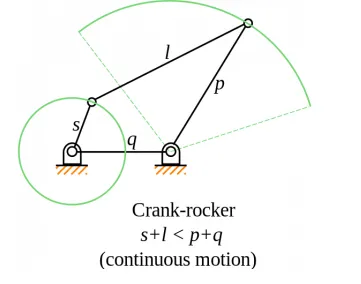
3. Crank and rocker mechanism
In crank and rocker mechanism, the shortest link “S’ is input crank or output crank. Input crank or output crank rotates 360°.
Grashof’s condition for double crank mechanism: s+l < p+ q
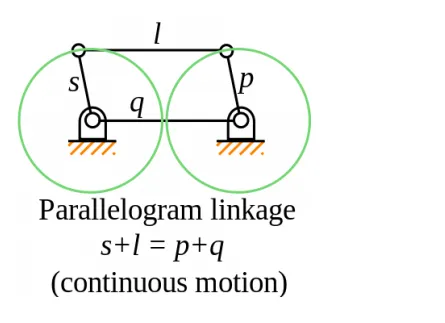
4. Parallel linkage mechanism
the parallel linkage mechanism is a special case of Grashof’s criteria, where the sum of the shortest link ‘S’ and longest link ‘L’ of a planar quadrilateral linkage is less than or equal to the sum of the remaining two links ‘P+Q’.
Grashof’s condition for parallel linkage mechanism: s+l = p+ q