Let ![]() be a homogeneous function of order
be a homogeneous function of order ![]() so that
so that
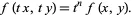 | (1) |
Then define ![]() and
and ![]() . Then
. Then
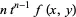 | 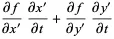 | (2) | |
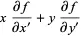 | (3) | ||
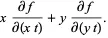 | (4) |
Let ![]() , then
, then
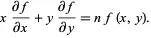 | (5) |
This can be generalized to an arbitrary number of variables
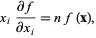 | (6) |
where Einstein summation has been used.
My WordPress Blog

Let ![]() be a homogeneous function of order
be a homogeneous function of order ![]() so that
so that
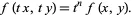 | (1) |
Then define ![]() and
and ![]() . Then
. Then
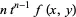 | 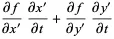 | (2) | |
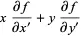 | (3) | ||
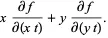 | (4) |
Let ![]() , then
, then
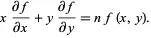 | (5) |
This can be generalized to an arbitrary number of variables
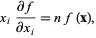 | (6) |
where Einstein summation has been used.
Comments are closed