This simple article shows how the Maclaurin series works, and how to write out the expansions. Although modern calculators are able to show the expansions, it is worth learning them for basic functions such as sin x and cos x.

The expansion above shows the general formula of the Maclaurin series. I have animated it to make it simpler for students to understand. The series is one of the easiest to understand in mathematics and very repetitive as you can imagine. If you are ever reading a scientific paper, you will find mathematicians making a meal of this one to make their work appear more complicated than it really is. I always have a chuckle when I see one of these dressed up.

I was just recently reading some of the original manuscripts of Madhava, and Srinivasa Ramanujan and the amazing thing I noticed was that they did not have fancy names for their formulas. They were simply looking for mathematical steps that would work every time. Moreover, they were relying heavily on intuition and foresight, which is actually very refreshing to see because that is the thinking process required to make progress in this field. Therefore, in this article I will avoid all the confusing jargon and get straight into the interesting stuff that works. Once you have understood the principle, you can call it whatever you like, get bogged down by terminology, and limits.

The Expansion

The series describes the steps required to convert any function f(x) into its equivalent series expansion. Many functions can be expressed as a series expansion, but not all. How will you know if a function has a series equivalent? If the function has derivatives then there is a good chance it may expand as a series. As long as the numerator part is not zero, it has a good chance, however, the only way is to have a go and find out. Usually, trigonometry functions such as sine, cosine, tangent, and natural log Ln may expand as a series. This is how digital calculators are able to give you the sine or cosine values of any angle.

All you have to do is to find the values of the bits in red and plug them into the series. The red bit are called the derivatives of the function and you simply find the derivative and set x to zero to find its value.

You may be wondering, “What is a derivative, and how do you find it?” That is the simple bit, because all you have to do is to differentiate the function, set x to zero in the differentiated equation and find its value, known as the coefficient. Once you have that, you simply plug it into the general formula.

Plugging the red bits into the Maclaurin general formula is the easy part. Sometimes differentiating a function to find its derivative can be the most challenging part. Therefore, if you have not learnt differentiation, then you will have to learn that first.

Maclaurin’s theorem is a specific form of Taylor’s theorem, or a Taylor’s power series expansion, where c = 0 and is a series expansion of a function about zero. The basic form of Taylor’s theorem is: n = 0 (f(n)(c)/n!)(x – c)n. When the appropriate substitutions are made

Maclaurin’s theorem is:

The Taylor’s theorem provides a way of determining those values of x for which the Taylor series of a function f converges to f(x).

In 1742 Scottish mathematician Colin Maclaurin attempted to put calculus on a rigorous geometric basis as well as give many applications of calculus in the work. It was the first logical and systematic exposition of the method of fluxions and originated as a reply to Berkeley’s attack on Newton’s methods of calculus. In this text, among several other monumental ideas, Maclaurin gave a proof of the theorem that today holds his name, Maclaurin’s theorem, and is a special case of Taylor’s theorem. He obtained this theorem by assuming that f(x) can be expanded in a power series form and then, upon differentiation and substituting x = 0 in the results, the values of the coefficients of each term can be obtained. He did this but did not investigate the convergency of the series at that time. Although this theorem holds Maclaurin’s name it was previously published by another Scottish mathematician, James Stirling, in his book Methodus Differentialis published in 1730. It is no doubt but that this theorem is what Maclaurin is best remembered.

A Maclaurin series is a Taylor series expansion of a function about 0,

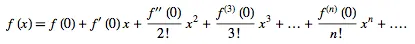
The Maclaurin series of a function up to order may be found using Series[f, x, 0, n ]. The th term of a Maclaurin series of a function can be computed in the Wolfram Language using Series Coefficient[f, x, 0, n ] and is given by the inverse Z-transform

Maclaurin series are a type of series expansion in which all terms are nonnegative integer powers of the variable. Other more general types of series include the Laurent series and the Puiseux series.

Maclaurin series for common functions include

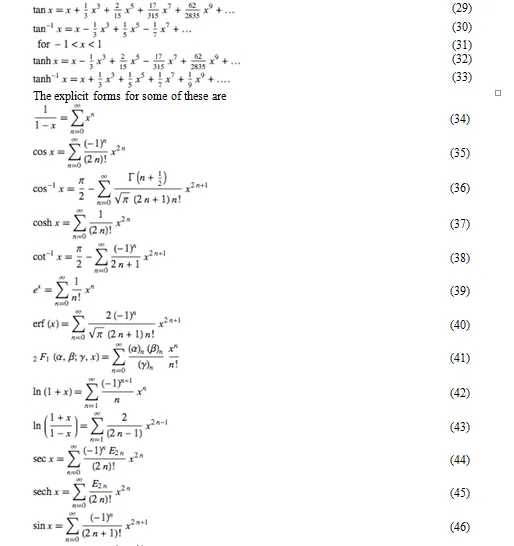
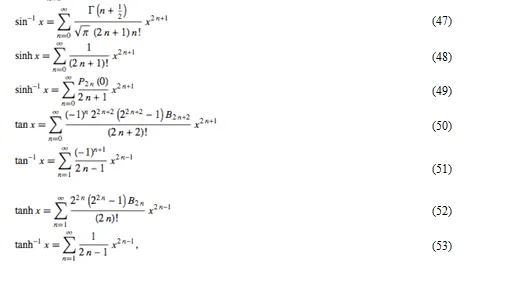
¬where is a gamma function, is a Bernoulli number, is an Euler number and is a Legendre polynomial