The product rule is used in calculus when you are asked to take the derivative of a function that is the multiplication of a couple or several smaller functions. In other words, a function f(x) is a product of functions if it can be written as g(x)h(x), and so on. Look at this example to get a better feel for it:

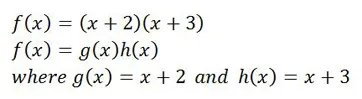This function is a product of two smaller functions.

Do you see how our f(x) is the product or multiplication of two smaller functions? We can also have a situation where our f(x) is the product of three or more smaller functions:

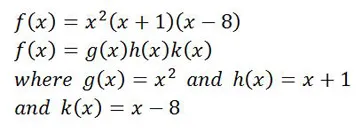This function is the product of three smaller functions.

When you see functions such as this, the product rule is there to help you derive them.

The Formula

The formula for the product rule looks like this for the product of two functions:

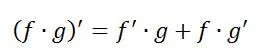The product rule formula.

If you have a product of three functions, the formula becomes the following:

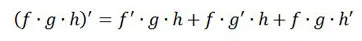The product rule formula for the product of three functions.

There is a pattern to this. Compare the two formulas carefully. Do you see how each maintains the whole function, but each term of the answer takes the derivative of one of the functions? So, for the product of two functions, we take the derivative of the first multiplied by the second and we add it to the derivative of the second multiplied by the first. For the product of three functions, we take the derivative of the first multiplied by the rest, then we add the derivative of the second multiplied by the rest, and then we add the derivative of the third multiplied by the rest, and so on. Do you see how we take the derivative of each successive smaller function while maintaining the larger function as a whole? Here are some examples for clarity.

Deriving Products of Two Functions

To derive products of two functions, we will use the first formula.

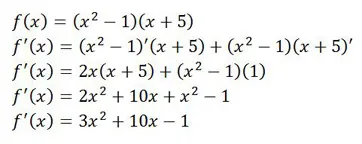Here is an example of how to derive the product of two functions.

Following the formula, we start by writing out our derivative, marking which of the smaller functions we need the derivative for in each term of our answer. Then, we go ahead and take the derivative of it while maintaining the other function for each term. After that, we multiply out and simplify.

Here is another example:

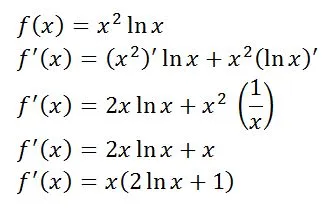Here is another example for deriving the product of two functions.

In this example, we have followed the same process. In this case, though, we have simplified our answer into factored form. When dealing with things such as logs, sine, cosine, and the like, the answer usually ends up in factored form, because that is the simplified form of writing those answers.