Surface tension as a name may refer to a cohesive force that inherently keeps the atoms and molecules of liquids bound together. The article helps to understand what surface tension is through practical examples and formulas.

A property caused due to the apparent tension effects or cohesion found within fluid molecules is called surface tension. Due to this, liquid particles show the tendency to cling with immiscible surfaces or at liquid or gas interfaces. Alternatively it may be understood as a surface energy existing freely at the interfaces of liquids.

With surface tension being a line force, it is normally expressed as force per unit length drawn across the free liquid surface.

The best example of liquid surface tension may be witnessed when a small ant becomes entangled in a drop of water, even with it being in just a drop of water: the ant has to struggle to free itself from the liquid due to the force of surface tension of water.

Measuring Surface Tension

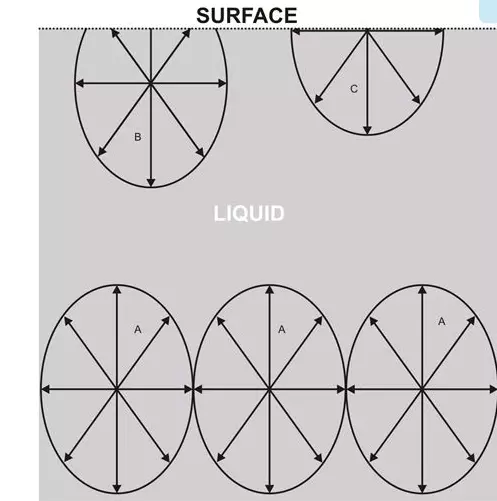
we see that a typical fluid molecule Amaintains a state of equilibrium due to the cohesive forces exerted by the adjoining molecules immediately surrounding A.

Since the cohesive forces exerted mutually by the adjacent molecules are equal and opposite in magnitudes, they cancel out the exertions so that the net or the resultant force over A becomes zero.

However, the molecules at the surface of the liquid exhibit greater cohesive forces downward, due to the absence of molecules above them. Therefore, the resultant cohesive force exerted over B will be acting more in the downward direction. This phenomenon makes liquid surfaces quite comparable to a stretched thin membrane.

Generally speaking surface tension may be quite negligible compared to with liquid pressures and gravitational force; however fluids enclosed within constricted areas or very narrow columns exhibit strong and significant cohesive tendencies, for example in capillary tubes, liquid drops, bubbles and liquid through porous materials.

When enclosed inside a vertical or inclined capillary, the rise and depressions of the liquid is termed as capillarity.

The phenomenon may be understood by relating the contact angle formed between the fluid and the capillary wall and the balancing force over the liquid column.

Referring to the figure shown below, it’s evident that acute contact angles between the liquid surface and the capillary wall constitutes a rise in the capillarity and vice versa, also the cohesive force of the liquid decreases with acute angles and increases with obtuse angles.

The above action with water and mercury becomes immaterial and irrelevant when enclosed in tubes and capillaries which are greater than 1 cm in diameter.

Measuring Surface Tension in Capillaries

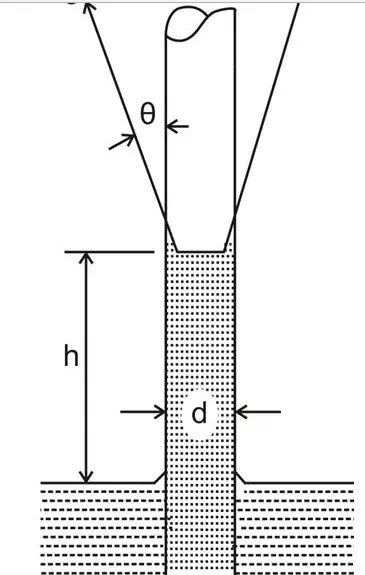
As explained in the previous section and referring the adjoining figure, we see a rise in the capillary where,

The force of upward tension = Weight of the liquid column in the tube,

The above expression can be formulated as:

πd.σ.cosθ = πd2.h.ρg/4

therefore, the capillary rise can be calculated as, h = 4σcosθ/ρgd, and the surface tension can be found by solving:

σ = hρgd/4cosθ

where σ = force due to surface tension per unit length, and,

θ = angle of contact between the tube wall and the liquid surface.

With water as the liquid and the tube made up of glass, θ ~ 0,

Therefore with water in a glass tube the capillary rise becomes:

h = 4σ/ρgd,

and the generated surface tension can be evaluated through the expression:

σ = hρgd/4

In case of a liquid droplet, the drop attains a pressure within the liquid enclosed which is equal to the exerted surface tension.

Equating the above forces we get, πd.σ = p.πd2/4

Finally, the formula for measuring surface tension in the above case becomes:

σ = p.d/4

where p = pressure and d = diameter of the droplet.

The above explanations help us to understand this important tendency associated with liquids and eventually relates to us regarding what surface tension is and how it can be measured.