Accurately predicting a ship’s draft is a necessary result of correctly applied hydrostatic principles but is far from sufficient. If the many items of weight on a ship are not distributed with considerable precision, the ship will float at unwanted angles of heel (sideways inclination) and trim(endwise inclination). Nonzero trim angles may lift the tips of propeller blades above the surface, or they may increase the possibility that the bow will slam into waves during heavy weather. Nonzero heel angles (which tend to be much greater than trim angles) may make all human activity aboard difficult; moreover, they are dangerous because they reduce the margin against capsizing. In general, the avoidance of such inclinations requires an extension of Archimedes’ principle to the first moments of weights and volumes: the collective first moment of all weights must equal the first weight moment of the water displaced.
The figure shows the cross section of a ship that is floating at heel angle θ, caused by the placement of a weight (w) a certain distance (d) from the centre line. At this angle, the upsetting moment, calculated as w × d × cos θ, is equaled by the righting moment Δ × GZ, (Δ is the symbol for displacement, and GZ is the distance from the centre of gravity [G] to the centre of buoyancy [Z]). Under these conditions, the ship is said to be in static equilibrium. If w is removed, the upsetting moment will become zero, and the righting moment will return the ship to its upright position. The ship is therefore judged to be stable. The moment will act in the stable direction only as long as the point M (the “metacentre,” the point where the buoyant force intersects the midplane) is above G (the centre of gravity of the ship and its contents). If M is below G, the forces of weight and buoyancy will tend to increase the angle of heel, and the equilibrium will be unstable. The distance from G to M, taken to be positive if M is above G, is called the transverse metacentric height.
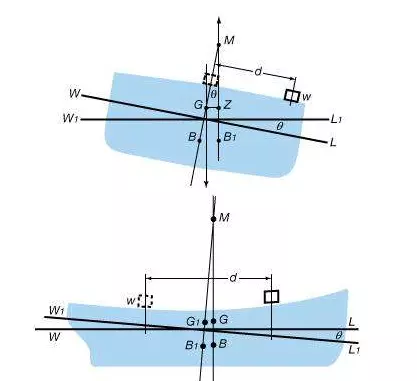
A value for metacentric height is usually found only for the zero heel condition; hence, it is an accurate measure of stability only for small disturbances—for example, ones that cause heeling of no more than about 10°. For larger angles, the “righting arm,” GZ, is used to measure stability. In any stability analysis, the value of GZ is plotted over the entire range of heel angles for which it is positive, or restoring. The resultant curve of statical stability shows thereby the angle beyond which the ship cannot return to upright and the angle at which the restoring moment is at a maximum. The area of the curve between its origin and any specified angle is proportional to the energy required to heel the ship to that angle.


